Le contrôle qualité est essentiel dans tout processus de production, qu’il s’agisse de bonbons, de pièces automobiles ou de logiciels. Mais voici une réalité incontournable : aucun test n’est parfait. Quand vous évaluez la qualité d’un lot en ne vérifiant qu’un échantillon, il y a toujours une part d’incertitude. Accepterez-vous un lot défectueux par erreur ? Rejetterez-vous un lot parfaitement bon ? Pour répondre à ces questions et maîtriser ces incertitudes, les courbes OC (Operating Characteristic Curves, ou courbes de contrôle opérationnel) entrent en jeu. Dans cet article, nous allons démystifier cet outil et montrer comment il permet de quantifier les incertitudes dans les contrôles qualité.
Les incertitudes en contrôle qualité : un défi universel
Imaginez que vous produisez des milliers de stylos par jour. Vérifier chaque stylo serait trop coûteux et chronophage, alors vous décidez de tester un échantillon de 50 stylos. Si moins de 2 stylos sont défectueux, vous acceptez le lot ; sinon, vous le rejetez. Simple, non ? Pas tout à fait. Ce plan d’échantillonnage comporte deux types d’incertitudes :
- Le risque du producteur (α) : Vous pourriez rejeter un lot de bonne qualité par erreur, juste parce que l’échantillon tiré n’était pas représentatif.
- Le risque du consommateur (β) : Vous pourriez accepter un lot de mauvaise qualité, parce que l’échantillon, par chance, ne contenait pas assez de défauts pour déclencher un rejet.
Ces risques traduisent l’incertitude inhérente à tout contrôle par échantillonnage. Mais comment les mesurer ? C’est là que les courbes OC deviennent indispensables.
Qu’est-ce qu’une courbe OC, concrètement ?
Une courbe OC est un graphique qui montre la probabilité d’accepter un lot en fonction de sa qualité réelle (exprimée, par exemple, en pourcentage de défauts). Elle agit comme une carte des incertitudes de votre plan de contrôle qualité.
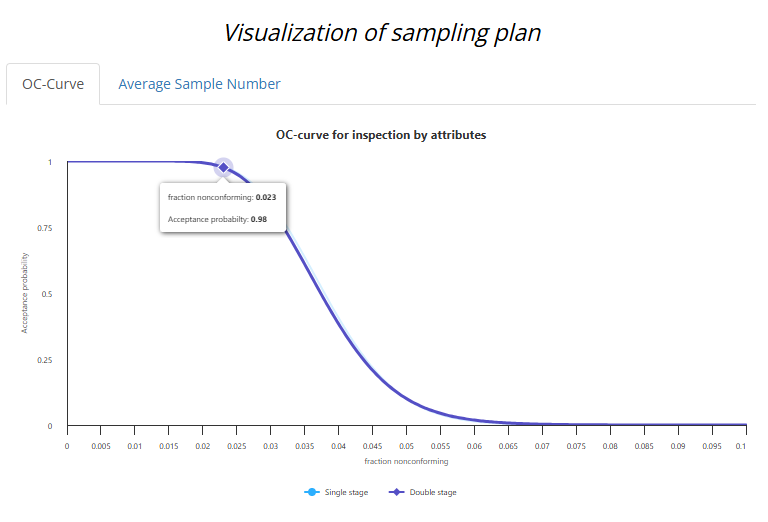
- Axe X (horizontal) : La proportion de défauts dans le lot (par exemple, 1 %, 5 %, 20 % de stylos défectueux).
- Axe Y (vertical) : La probabilité d’accepter le lot (de 0 à 1, ou 0 % à 100 %).
- La courbe : Elle descend généralement. Plus le lot est défectueux, moins vous avez de chances de l’accepter.
Prenons un exemple concret :
- Votre règle est : « Je teste 50 stylos, et j’accepte le lot s’il y a 1 défaut ou moins. »
- La courbe OC pourrait vous indiquer :
- Si le lot a 2 % de défauts, vous l’acceptez dans 95 % des cas.
- Si le lot a 10 % de défauts, la probabilité d’acceptation chute à 20 %.
Cette courbe vous donne une vision claire : elle quantifie les chances de « succès » (ou d’erreur) de votre test selon la qualité du lot.
Quantifier les incertitudes avec la courbe OC
Les courbes OC ne se contentent pas de décrire un test ; elles permettent de mesurer précisément les risques α et β. Voici comment :
- Définir une qualité acceptable (AQL) : C’est le seuil maximal de défauts que vous tolérez (par exemple, 1 %). Sur la courbe OC, regardez la probabilité d’acceptation à ce niveau. Si elle est de 95 %, cela signifie que vous rejetez 5 % des lots corrects par erreur. Ce 5 % est votre risque du producteur (α).
- Définir une qualité inacceptable (LQL) : C’est le seuil où le lot est jugé trop mauvais (par exemple, 10 % de défauts). Si la courbe montre une probabilité d’acceptation de 10 % à ce niveau, cela signifie que 10 % des lots défectueux passent à travers les mailles du filet. Ce 10 % est votre risque du consommateur (β).
En jouant sur la taille de l’échantillon (50 stylos, 100 stylos…) ou le critère d’acceptation (1 défaut max, 2 défauts max…), vous pouvez ajuster la courbe OC pour réduire ces risques selon vos priorités.
Pourquoi les courbes OC sont-elles si puissantes ?
Elles transforment l’incertitude, qui peut sembler abstraite, en quelque chose de tangible et mesurable. Voici leurs avantages :
- Pour le producteur : Vous évitez de gaspiller des lots corrects en comprenant le risque α.
- Pour le client : Vous limitez les lots défectueux qui arrivent sur le marché grâce au risque β.
- Pour tous : Elles permettent d’optimiser le contrôle qualité en trouvant le bon équilibre entre coût (taille de l’échantillon) et fiabilité.
Une courbe OC « raide » (qui passe rapidement de 100 % à 0 % d’acceptation) indique un test très discriminant, capable de bien séparer les bons lots des mauvais. Une courbe « plate », en revanche, révèle un test peu fiable, avec beaucoup d’incertitude.
Comment construire une courbe OC ?
Pas besoin d’être un statisticien pour comprendre le principe de base :
- Choisissez votre plan : Taille de l’échantillon (n) et nombre maximal de défauts acceptés (c).
- Utilisez une formule statistique : La probabilité d’acceptation suit souvent une loi binomiale ou une approximation (comme la loi de Poisson pour les grands lots). Par exemple, pour un lot avec p % de défauts, calculez la probabilité d’avoir c défauts ou moins dans n unités.
- Tracez la courbe : Calculez cette probabilité pour plusieurs valeurs de p (0 %, 1 %, 5 %, etc.) et reliez les points.
Aujourd’hui, des logiciels ou des tableurs comme Excel peuvent faire ces calculs pour vous. Mais l’essentiel est de comprendre ce que la courbe vous raconte sur vos incertitudes.
Le site https://www.acceptancesampling.com/ propose également des calculs de courbe poussés.
En conclusion : maîtriser l’incertitude pour mieux décider
Les courbes OC ne suppriment pas les incertitudes – elles les rendent visibles et quantifiables. Elles vous aident à répondre à des questions cruciales : « Mon test est-il trop strict ? Trop laxiste ? Puis-je faire confiance à mes résultats ? » En démystifiant cet outil, vous gagnez en contrôle sur votre processus qualité, que vous soyez producteur ou consommateur. Alors, la prochaine fois que vous testerez un échantillon, pensez à la courbe OC : elle est votre alliée pour transformer l’incertitude en décision éclairée.






